Atmosphere Model Aeolus 2.0

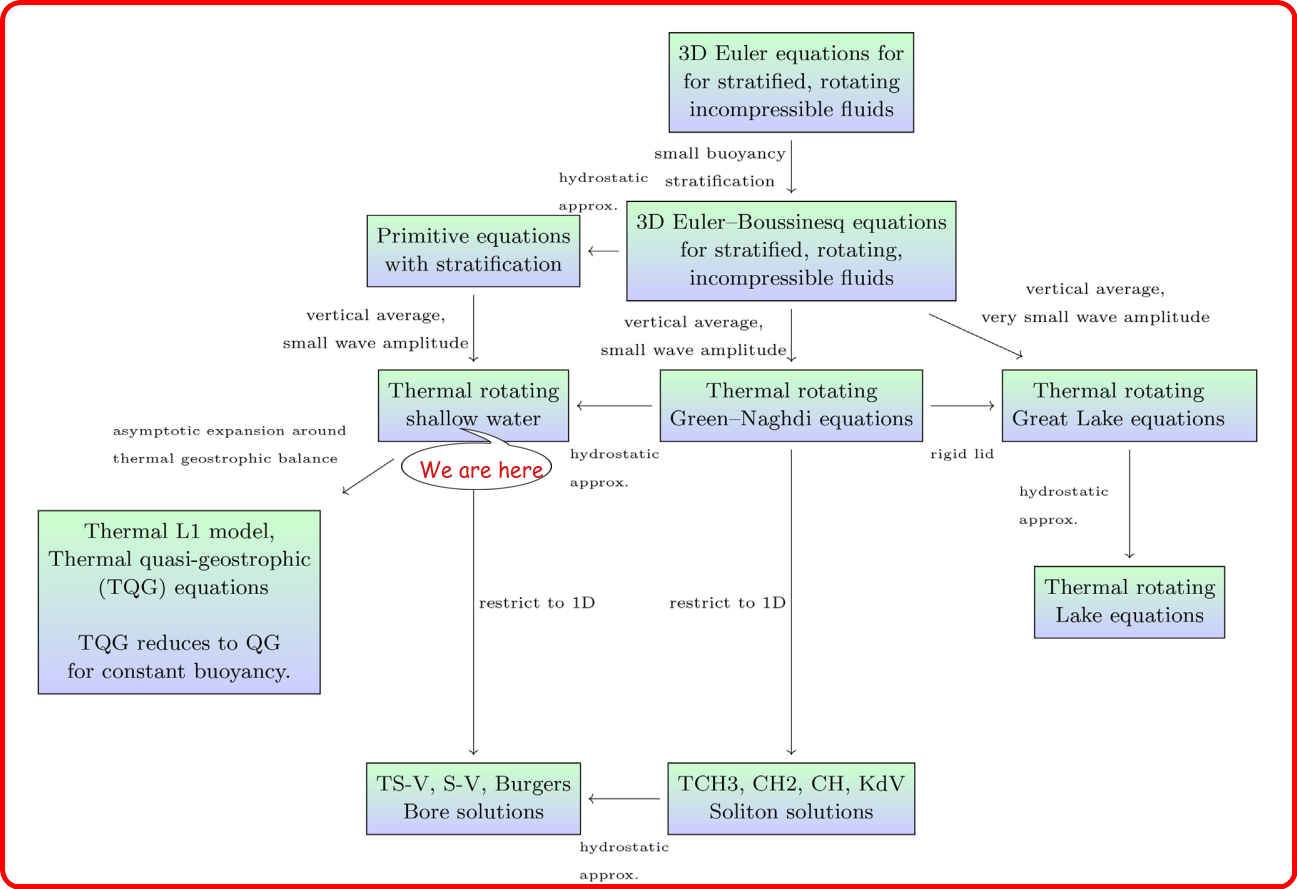
Model Description

Aeolus 2.0 is an in-house open-source numerical model designed to simulate atmospheric circulations. The model's dynamical core is based on a multi-layer pseudo-spectral moist-convective Thermal Rotating Shallow Water (mcTRSW) model. The Dedalus algorithm, renowned for its handling of spin-weighted spherical harmonics, manages the pseudo-spectral problem-solving tasks. One advantage of spin-weighted spherical harmonics is that differentiation on the sphere remains regular everywhere. In the classical setup of shallow-water models, the fluid is homogeneous, incompressible, and under hydrostatic balance. Therefore, gradients of mean temperature and density are invariant in this setup. However, the TRSW model employs inhomogeneous layers, allowing horizontal variations in potential temperature.  The elucidation of the multi-layer Thermal Rotating Shallow Water (TRSW) model and its associated moist convection, characterized by minimal parameterization across the entire spherical domain, has been comprehensively detailed in the publication by Rostami et al., 2022.

The model captures the temporal and spatial evolution of vertically integrated potential temperature, pressure, water vapor, precipitation, and the intricate influence of bottom topography. It comprehensively characterizes velocity fields in both the lower and upper troposphere, employing resolutions spanning a spectrum from smooth to coarse. This enables the exploration of a wide range of dynamic phenomena with varying levels of complexity.

Layer versus Level Models

Another feature of Aeolus 2.0 is that it is a layer model. Layer models and level models are two approaches used in geophysical fluid dynamics to represent the vertical structure of the atmosphere and oceans. While level models incorporate thermodynamics easily, they are less accurate than layer models, especially at high vertical modes. The difference lies in how these models represent the density profile. In a level model, density is assumed to be continuously stratified, and finite differencing is used at fixed depths. In contrast, a layer model approximates the continuous density profile with a piece-wise constant profile, where the depth of the interfaces can vary with position and time. Accuracy issues in level models arise from the inherent limitations of finite differencing at small scales. In contrast, layer models do not suffer from this problem because the piece-wise constant density profile is physically valid, and the equations of motion precisely represent this particular stratification. The Laplace tidal equations serve as a prominent example that highlights the disparity between layer and level models. These equations, which describe the behavior of tides in the ocean and atmosphere, are a one-layer model with no counterpart in the level model family.

Spin-Weighted Spherical Harmonics

In the numerical methodology employed in Aeolus 2.0, the Dedalus algorithm is utilized. The Dedalus algorithm incorporates the use of spin-weighted spherical harmonics, as documented in the works of Vasil et al. (2019)  and Lecoanet et al. (2019). Spin-weighted spherical harmonics were originally introduced by Gelfand and Shapiro (1956) in their studies related to the Lorenz group. One key advantage of utilizing spin-weighted spherical harmonics in combination with spinor basis vectors is the ability to perform differentiation operations on the spherical domain in a manner akin to Fourier series operations. This property enables regular and well-behaved diagonal wavenumber multiplication across the entire sphere, eliminating the necessity for traditional singular gradients at the poles. This advantageous feature enhances the numerical stability and accuracy of calculations performed within the mcTRSW dynamical core on a spherical domain.

References