Bootstrapping, Resampling, Uncertainty Visualization

Resampling and Bootstrapping

Looking for someone to explain this to me in terms I can understand on a Sunday I found Christina Knudson’s youtube channel where she does exactly that in small, easily digestible chunks. Thanks! After watching this 5 part series on bootstrapping is turns out that bootstrapping really just means resampling a random sample with replacement at the same size as the original sample.

Or, in the words of the rsample help: A bootstrap sample is a sample that is the same size as the original data set that is made using replacement. This results in analysis samples that have multiple replicates of some of the original rows of the data.

Bootstrapping is used, for example, to estimate the uncertainty of statsitical properties of a sample without having to make a lot of assumptions about it (e.g. distribution type, sample size, etc).

There are lots of different r packages to do resampling and bootstrapping but it so happens that Alex Hayes, in his talk about the spectacular broom package at the same rstudio conference uses the rsample package from the tidymodels family to bootstrap. So this seems a good choice.

With this, creating a numer of bootstrap samples using the mtcars dataset is straightforward.

library(tidyverse)
library(rsample)

samples = 1000
boots = bootstraps(mtcars, times=samples)
head(boots)

## # A tibble: 6 x 2
##   splits          id           
## * <list>          <chr>        
## 1 <split [32/14]> Bootstrap0001
## 2 <split [32/13]> Bootstrap0002
## 3 <split [32/10]> Bootstrap0003
## 4 <split [32/12]> Bootstrap0004
## 5 <split [32/13]> Bootstrap0005
## 6 <split [32/8]>  Bootstrap0006

boots is a compact but somewhat daunting return value. It is a tibble that contains a list column (splits) and an id column. The id column simply holds an identifier for the bootstrap resample. splits is a list of length 4 where the first element points to the original data set, the second holds the indices of the resample and the rest are irrelevant (at this point). So the pointer to the original data frame in the first row could be accessed like this boots$splits[[1]]$data. This is really fast because (as I understand it) nothing is created or copied yet. We have a pointer to the original data and a vector of integers with the sampled indices.

To replicate Christina’s example in the video, I want to simply bootstrap to estimate the density distribution of the mean of the wt variable. To do this, I need to calculate the mean for wt for each bootstrap of the 1000 samples.

Because I want to do this for each resample and boots$splits is a list column the purrr package will be helpful if I want to avoid writing lots of loops or, god forbid, use the l/s/apply functions which I have regrettably never become friends with. If you are unfamiliar with purrr, Charlotte Wickham’s tutorial is a great place to start, especially considering that I am only linking videos today.

The first step in figuring out how to map something with purrr is to figure it out for a single row. What I am doing now comes with no guarantees for efficiency. What I want is the actual data frame for the resample (not just an index vector and a pointer to the original data currently in splits). Conveniently, the somewhat cryptically named analysis function in the rsample package does just that.

bootstrap_sample = analysis(boots$splits[[1]])
head(bootstrap_sample)

##                   mpg cyl  disp  hp drat    wt  qsec vs am gear carb
## Merc 280C        17.8   6 167.6 123 3.92 3.440 18.90  1  0    4    4
## Merc 230         22.8   4 140.8  95 3.92 3.150 22.90  1  0    4    2
## Toyota Corona    21.5   4 120.1  97 3.70 2.465 20.01  1  0    3    1
## Fiat X1-9        27.3   4  79.0  66 4.08 1.935 18.90  1  1    4    1
## Dodge Challenger 15.5   8 318.0 150 2.76 3.520 16.87  0  0    3    2
## Lotus Europa     30.4   4  95.1 113 3.77 1.513 16.90  1  1    5    2

So calculating the mean of wtin the first resample would work simply like this:

mean(analysis(boots$splits[[1]])$wt)

## [1] 2.929

To generalize this to the purrr recipe for all resamples I simply replace the first element [[1]] by .x.

boots_mean = boots %>%
  mutate(mn = map_dbl(splits, ~ mean(analysis(.x)$wt)))

head(boots_mean)

## # A tibble: 6 x 3
##   splits          id               mn
## * <list>          <chr>         <dbl>
## 1 <split [32/9]>  Bootstrap0001  3.46
## 2 <split [32/12]> Bootstrap0002  3.10
## 3 <split [32/13]> Bootstrap0003  3.55
## 4 <split [32/13]> Bootstrap0004  2.96
## 5 <split [32/8]>  Bootstrap0005  3.06
## 6 <split [32/13]> Bootstrap0006  3.14

Having added the column containing all the bootstrap sample means, I can use ggplot to approximate the sample distribution of the mean.

boots_mean %>%
  ggplot(aes(mn)) +
  geom_density() +
  labs(title = "Approximated sampling distribution of mean wt",
       x = "mean wt",
       y = "frequency") +
  theme_minimal()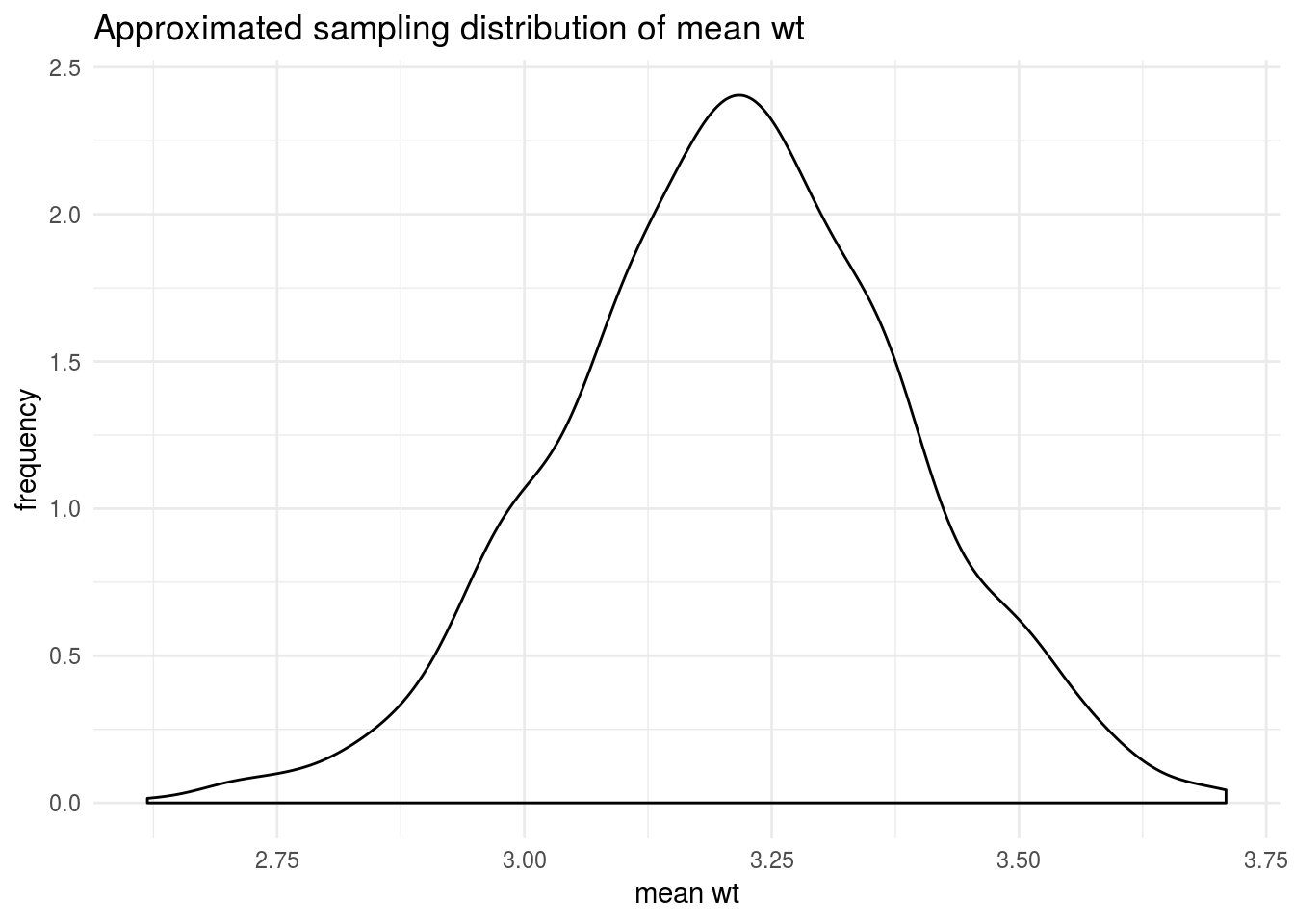

For completeness sake I am also replicating Alex’ example here where he uses boostrapping and the augment function of the broom package to visualize the uncertainty of a model fit.

His example is the relationship between mpg and wt in mtcars.

mtcars %>%
  ggplot(aes(wt,mpg)) +
  geom_point() +
  theme_minimal()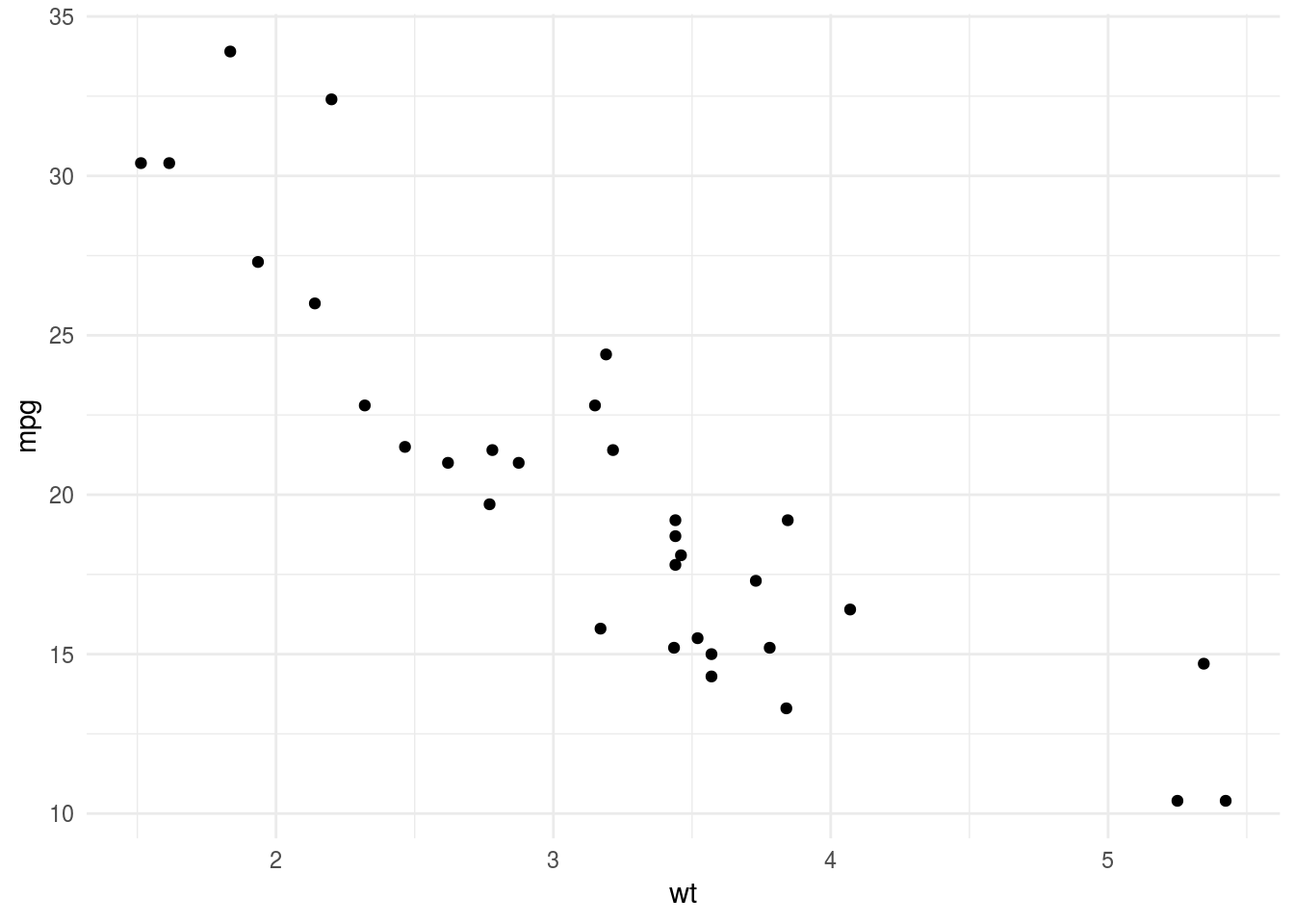

Again, first working things out for a single case to feed to purrr, we construct the helper function fit_nls_on_bootstrap that fits a nonlinear model to boots. We also map tidy model coefficients k and b.

fit_nls_on_bootstrap <- function(split) {
  nls(
    mpg ~ k / wt + b,
    analysis(split),   
    start = c(k = 1, b = 0)
  )
}

boots_fit = boots %>%
  mutate(fit = map(splits, fit_nls_on_bootstrap),
         coef_info = map(fit, tidy))

head(boots_fit)

## # A tibble: 6 x 4
##   splits          id            fit       coef_info       
## * <list>          <chr>         <list>    <list>          
## 1 <split [32/14]> Bootstrap0001 <S3: nls> <tibble [2 × 5]>
## 2 <split [32/13]> Bootstrap0002 <S3: nls> <tibble [2 × 5]>
## 3 <split [32/10]> Bootstrap0003 <S3: nls> <tibble [2 × 5]>
## 4 <split [32/12]> Bootstrap0004 <S3: nls> <tibble [2 × 5]>
## 5 <split [32/13]> Bootstrap0005 <S3: nls> <tibble [2 × 5]>
## 6 <split [32/8]>  Bootstrap0006 <S3: nls> <tibble [2 × 5]>

This returns an even more frightening thing than before. Fortunately, we can use unnest to flatten this horrendous thing into something more sane.

boots_coefs = boots_fit %>%
  unnest(coef_info)

head(boots_coefs)

## # A tibble: 6 x 6
##   id            term  estimate std.error statistic  p.value
##   <chr>         <chr>    <dbl>     <dbl>     <dbl>    <dbl>
## 1 Bootstrap0001 k        43.3       5.20      8.33 2.69e- 9
## 2 Bootstrap0001 b         5.72      1.93      2.96 5.92e- 3
## 3 Bootstrap0002 k        46.3       4.12     11.2  2.91e-12
## 4 Bootstrap0002 b         3.91      1.42      2.75 1.00e- 2
## 5 Bootstrap0003 k        38.9       3.93      9.89 5.95e-11
## 6 Bootstrap0003 b         6.64      1.45      4.59 7.31e- 5

And plot the histograms for k and b:

boots_coefs %>%
  ggplot(aes(estimate)) +
  geom_histogram(binwidth = 2) +
  facet_wrap(~ term, scales = "free") +
  labs(title = "Approximated sampling distributions of k and b",
       x = "value",
       y = "count") +
  theme_minimal()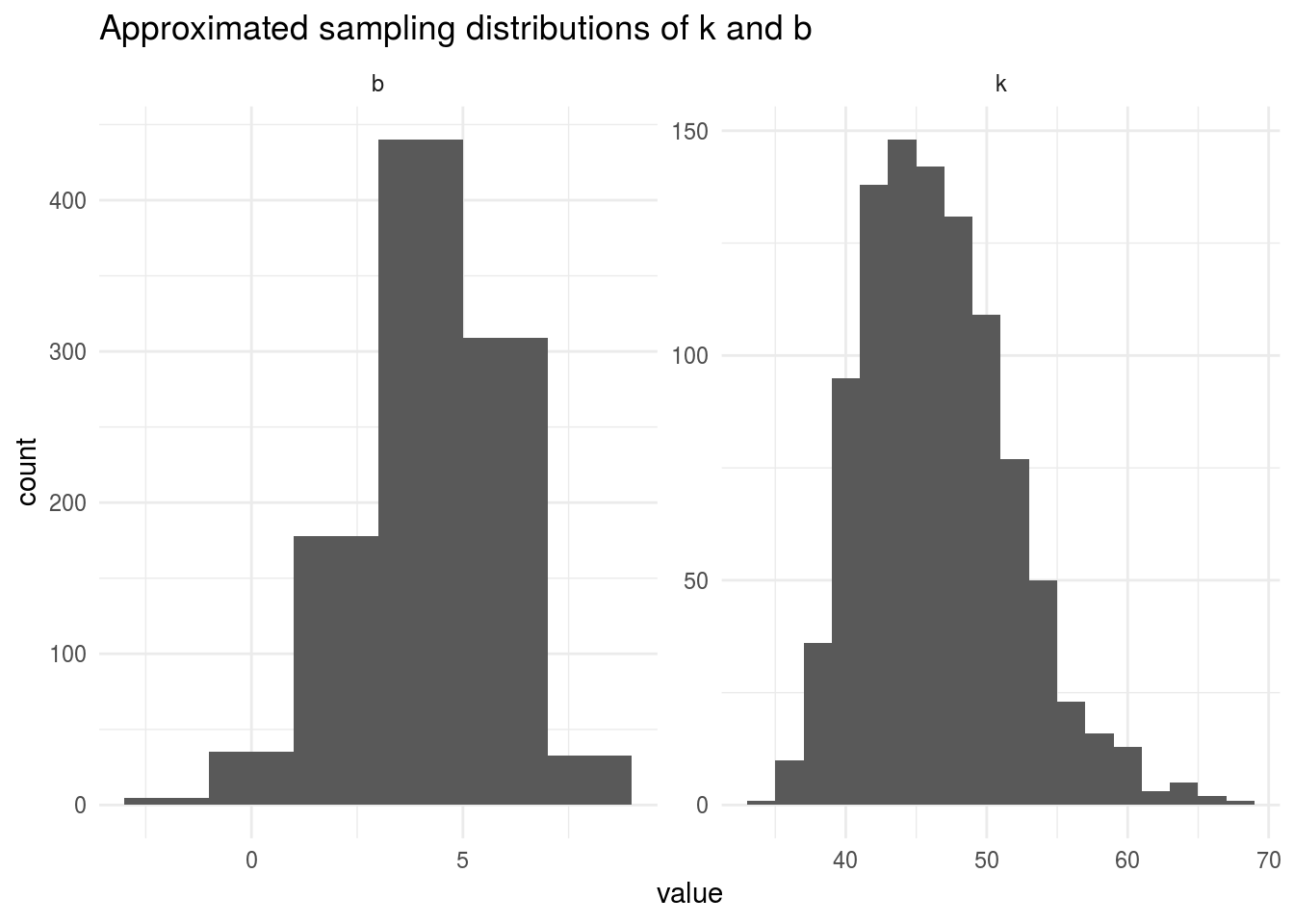

Finally, we use broom::augment to get fitted values from each model and plot the fits of the first 100 bootstrap samples.

library(broom)
boot_aug = boots_fit %>%
  mutate(augmented = map(fit, augment)) %>%
  unnest(augmented)

boot_aug %>%
  filter(id %in% unique(boot_aug$id)[1:100]) %>%
  ggplot(aes(wt, mpg)) +
  geom_point() +
  geom_line(aes(y=.fitted, group=id),alpha=0.1) +
  theme_minimal()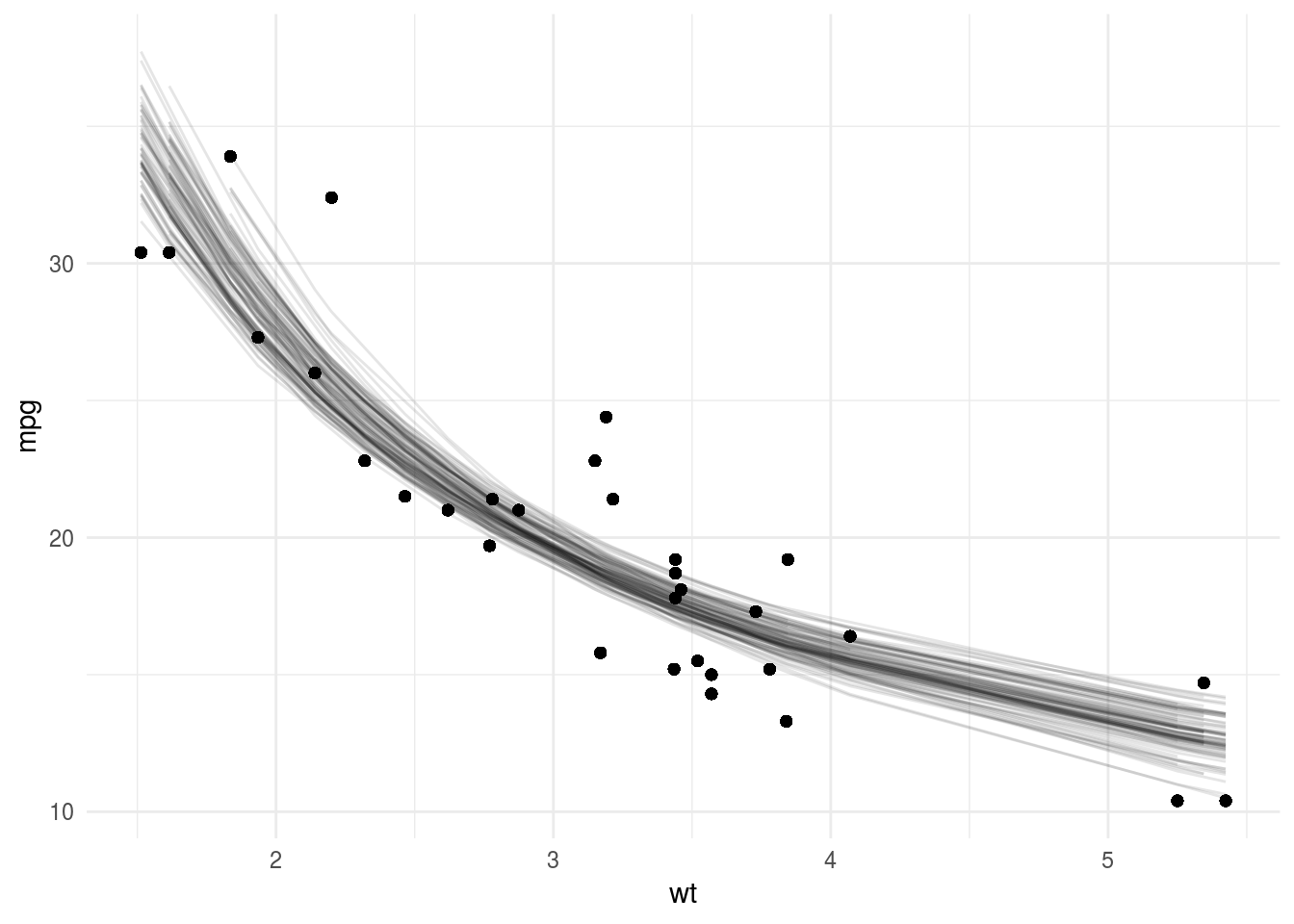

Sadly, it seems the ungeviz package has to wait for another day…