The productivity of the vegetation is a function of C, N, and T alone.
As in [9] we assume that the productivity function P(C,N,T) can be presented in
the multiplicative form (accordingly with Liebig's principle):
where 
is the maximum productivity of the vegetation and 
,
are functions: 
.
Here 
is a unimodular function: 
(see Fig. 2),
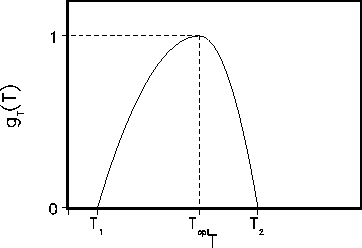
Figure 2: Function describing the dependence of productivity on temperature T.
according to [10], the function 
is a monotonous increasing function with
saturation (see Fig. 3).
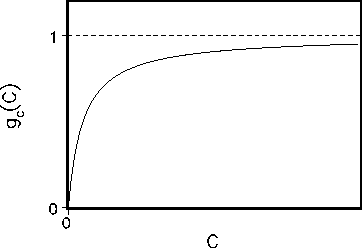
Figure 3: Function describing the dependence of productivity on carbon content C in the atmosphere.
The function 
is a monotonous increasing function, tending to one when
(as in Fig. 3). Since C=A-N then the product
can be presented in the form 
for fixed A(t) (see Fig. 4).
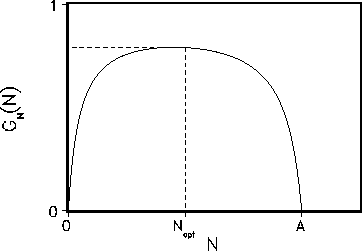
Figure 4: The function 
as a function of N.
The function 
is a unimodular function where 
. It is defined
in the interval 
.