Caldeira and Kasting[1] have calculated the life span of the biosphere under the
assumption that the weathering
rate 
is always equal to the present value 
. This is
clearly a rather
rough approximation.
We call this approach the geostatic model (GSM). Berner et al.[22] already emphasized the
impact of
the global weathering rate, the sea-floor spreading rate, and the continental area, respectively,
on the global climate.
In the framework of a dynamic-equilibrium approach for the global carbon
cycle at longer time scales (
a), Walker et al.[7] first proposed a balance between
the CO
sink in the atmosphere-ocean system and the metamorphic (plate-tectonic)
source. The
sources of CO for the atmosphere-ocean system are sea-floor spreading at the mid-ocean
ridges
and back-arc or andesitic volcanism. Both processes depend on the spreading rate S
(see, e.g., [23]).
In most of the models for the volatile exchange between mantle and surface reservoirs [45, 30, 31]
the mantle degassing as the source of
CO for
the atmosphere-ocean system is proportional to the so-called degassing volume beneath
mid-ocean
ridges. This degassing volume depends linearly on the spreading rate S. The sink for
CO in the
atmosphere-ocean system is, on the other hand, related to the weathering rate
and the continental area 
(available for weathering). Rock weathering happens on the continents. The weathering
products are transported to the ocean and deposited exclusively as pelagic carbonates on the
seafloor. In this way our model provides an upper limit for subduction of carbonates because
we do not consider shallow water carbonate burial [51, 25, 26].
There is no doubt about the importance of hydrothermal reactions, especially in late Hadean and
early Archaean. However, the present fluxes of basalt seawater exchange are at least one order
of magnitude lower than the river dissolved fluxes from continental weathering
[55, 56]. Hydrothermal fluxes are modelled proportional to the seafloor spreading
rate. In the future the decreasing spreading rates result in decreasing hydrothermal fluxes.
Because of our time window (Proterozoic - 3.5 Ga in planetary future) we can neglect these processes.
Therefore, in a well-justified linear
approximation, the dynamic equilibrium
of CO fluxes may be expressed as a relation between dimensionless quantities
[37]:
where 
is the weathering
rate normalized by the present value,
is the continental area normalized by the present value, and
is the spreading rate normalized by the present value.
The ratio 
is called the ``Geophysical Forcing Ratio'' (GFR). This ratio
describes the influence of volcanic activities (proportional to S) and the continental
area on the global climate [13] in a nutshell.
Now we have all the means to calculate the weathering rate from geodynamical theory, and with the help of Eq. 1 we can determine self-consistently the climate parameters mentioned above. Eq. 10 has been used by various authors (e.g. [22, 42, 44, 41, 11, 24, 33]) to study the influence of sea-floor spreading and continental area on weathering. Franck et al.[23] were the first group using geodynamical theory to couple the two forcing functions of continental area and spreading, which were generally considered independently by previous geochemistry and climate modellers. This introduces an additional interaction into the system, as will be shown below.
The global carbon cycle is part of the general process of volatile exchange which has taken
place
throughout the Earth's history. In the models of Jackson and Pollack[36],
McGovern and Schubert[45], Williams and Pan[54], and Franck and Bounama[30, 31], this
volatile
exchange has been studied in great detail. The main idea consists in the coupling of the
thermal and the degassing
history of the Earth. To formalize this coupling we need a relation between the mantle heat
flow, expressing the thermal history, and the sea-floor spreading rate, characterizing tectonics
and volatile exchange. According to boundary layer theory, this spreading rate is given as a
function of the mantle heat flow calculated by the cooling process of an oceanic plate which
is approximated by the cooling of a semi-infinite halfspace. The derivation of this formula is
given in the well-known textbook on geodynamics by Turcotte and Schubert[50]:
Here 
is the mean heat flow from the mantle, S is again the sea-floor spreading rate,
k is the thermal
conductivity, 
is the average mantle temperature, 
is the surface temperature
which is taken as
the constant outer temperature of the upper boundary layer in the parameterized convection
approximation, 
is the thermal diffusivity, and 
is the area of ocean basins at
time t. The evolution of the global average mantle heat flow is a result of the parameterized
convection model. It is in good agreement with the secular mantle cooling of about 250 K
within the last 3 Ga derived from the investigations of komatiites [29].
The area of the Earth`s surface, 
, is obviously the sum of and the area of
continents, 
,
i.e.,
Eqs. 11 and 12 can be used to introduce continental-growth models into the equations for the volatile cycle.
The continental crust is especially diverse and heterogeneous, and its formation is less understood than that of the geologically relatively simple oceanic crust. Two different hypotheses have been suggested to explain the evolution of the continental crust. The first proposes that the present continental crust formed very early in the Earth's history and has been recycled through the mantle in steadily decreasing fashion such that new additions are balanced by losses, resulting in a steady-state system [32, 2, 48]. The return of the continental material to the mantle and its replacement by new younger additions reduce its mean age, both of which keep the mass of the continents constant. The second hypothesis proposes crustal growth throughout geological time without recycling into the mantle. In modern studies (see [49]), there is a growing appreciation of the observation that the continental crust grows episodically, and it is concluded that at least 60% of the crust have been replaced by the late Archaean. In the present paper we use a continental-growth model that is based on geological investigations [27] of the best-studied regions, North America and Europe, which formed a single land mass for most of the Proterozoic. Our empirical continental-growth model is depicted in Fig. 1. This data-based description is clearly more realistic than the theoretical models recently used by Franck et al.[23].
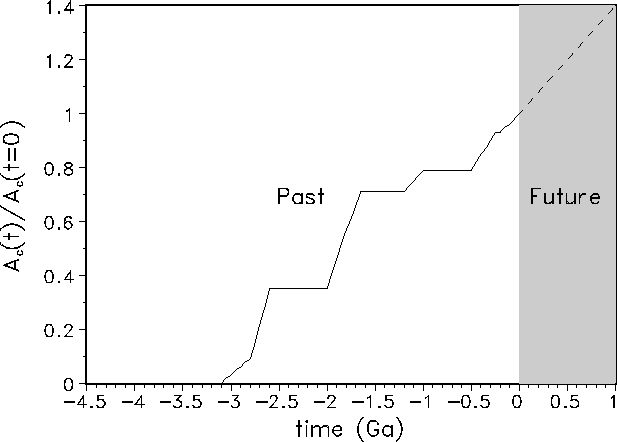
Figure 1:
Cumulative continental crust growth model derived from the best studied region,
North
America and Europe, according to Condie[27]. Note that crustal growth had two
major
pulses in the Archaean and Proterozoic. The continental area is normalized to the
present value 
. Future values are estimated by a linear extrapolation (dashed line).
As with many other authors, we assume that continental growth is the growth of the continental area. This continental area is directly related to the weathering process.