1. Introduction

The Climate Change Problem is very fashionable today. A huge amount of publications mask some simple facts that we can hardly conceive:

• How does the biosphere machine operate?
• Is the Earth biosphere unique, or do there exist other virtual biospheres?

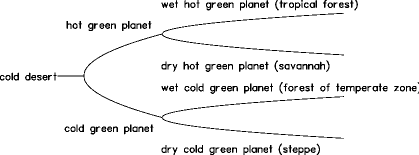
A few words about the history of this problem. It was initially formulated (at a qualitative level, of course) by Vernadsky (1927) in the form of an idea about the interdependence between vegetation and climate. Then Kostitzin (1935) realized this idea in the first mathematical model for the coevolution of atmosphere (climate) and biota. It is interesting that he has obtained the "epoques glaciaires" as self-oscillations in this model. Recently Watson and Lovelock (1983) further developed Vernadsky's idea. They considered a causal loop between the surface temperature and two types of vegetation (differing in albedo). A competition between them on a temperature ecological niche generates different spatial vegetation and temperature patterns ("Daisy World"). In 1993 Schellnhuber and von Bloh realized this model, using cellular automata, in the form of a 2-dimension structure. This approach showed an important role of fluctuations in forming spatial patterns (von Bloh et al., 1997).

Svirezhev (1994) formulated a concept of "virtual biospheres". According to this concept the contemporary Earth biosphere is one of many possible (virtual) biospheres corresponding to different equilibria of a nonlinear dynamical "climate + biosphere" system (Svirezhev and von Bloh, 1999). In the course of the planetary history and own evolution, this system passed through several bifurcation points in which some random factors (small perturbations) determined solution branches actually followed by the system. A driving force in this evolution could be the evolution of the "Earth green cover", which had, in turn, several bifurcation points, for instance, the appearance of terrestrial vegetation, or the change from the coniferous forest to the deciduous forest. Note that this concept contradicts Vernadsky's "ergodicity axiom", according to which the contemporary Earth biosphere is unique, irrespective of the initial and previous states.

What kind of bifurcations are admissible in this system? We can observe a change of planet's "status" from a "cold desert" to either a "cold green planet", or a "hot green planet" (the first bifurcation). Then either a "wet hot" planet covered with a tropical rain forest, or a "dry hot" planet (savannah) develops from a "green hot" planet as a result of the second bifurcation. Analogically, either a "wet cold" (a temperate forest) or a "dry cold" (steppe) planet arises from a "green cold" planet (see Fig. 1).

Fig. 1: Bifurcation diagram for the "climate+biosphere" system.

2. Minimal models

A so-called minimal model describing the climate biosphere mechanisms of a hypothetical zero-dimensional point planet is presented in (Svirezhev and von Bloh, 1996). Unlike other attempts of modelling the global vegetation (e.g., the Osnabrück biosphere model (Esser, 1991) or the Frankfurt biosphere model (Lüdeke et al., 1995)) the system can be fully understood through analytical as well as numerical inspections. This model consists of two coupled differential equations and is based on two hypotheses:

Hypothesis 1:

The albedo α depends only on the vegetation density N, so that α=α(N) is a monotonous decreasing function of N.

and

Hypothesis 2:

The growth function β depends only on temperature T, i.e. β=β(T); it is an unimodular function of T.

The dynamics of coupled climate-vegetation can be described by two coupled differential equations:

dT(t)/dt=S(1-α(N))-4σT⁴
dN(t)/dt=β(T)N-γN².

The evolution of climate is determined by the balance between ingoing (S(1-α))and outgoing radiation (4σT⁴), while the evolution of the vegetation is determined by the balance between growth (&beta(T)N) and decay (γN²). Stationary solutions can be determined by setting the right-hand side of the equations to zero:

dT(t)/dt=0
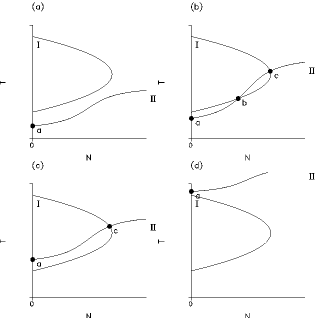
dN(t)/dt=0.

Analytical calculations for this coupled climate-biosphere system indicate that up to two different stable equilibria are possible. One is the "dead" planet without any vegetation (N=0) and the other is the living planet (N>0) (see Fig. 2).

Fig. 2: Zeros of the two differential equations (I) and (II) in the climate-vegetation domain {T,N} for different insolations. The intersections of the two curves indicate stationary points and are marked with a-c.

Further on a carbon cycle was added to the system of two differential equations (Svirezhev and von Bloh, 1997) increasing the number of equations to three. Because the total amount of carbon A is conserved the set of equations can be reduced by one. The system has two causal loops: (1) vegetation → albedo → temperature → vegetation, (2) vegetation ↔ atmosphere carbon → temperature → vegetation. In this case the system can have up to five different equilibria: three of them are stable and two others are unstable. The projection of its phase portrait onto the climate vegetation plane is shown in Fig. 3. Two bifurcation parameters can be identified, A and the maximum biological productivity P_max. Depending on these two parameters the "living" planet bifurcates into the "hot green" planet and the "cold green" planet.

Fig. 3: Phase portrait of the climate-biosphere system with carbon cycle. The different colors indicate the basins of attraction of the three stable equilibria "cold desert", "cold green planet", and "hot green planet".

There are four attractive domains corresponding to the following equilibria:

1. "cold desert" when the planet has no vegetation and the planetary temperature is less than -3°C.
2. "cold green planet" with a rich vegetation and relatively low temperature, approximately equal to the current Earth's temperature, 15°C.
3. "hot green planet" with a poor vegetation and relatively high temperature, higher than 30°C that is typical for Earth's hot deserts.
4. "hot desert" is a lifeless planet, its temperature is higher than the upper boundary of the tolerable interval (>60°C).

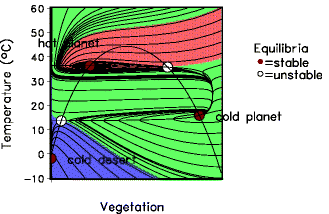
Let us consider the evolution of the system topology when the total amount of carbon slowly decreases. An animation is available as a MPEG video(3 MByte). Fig. 4 plots the temperatures of the different equilibria as a function of A, where the black lines indicate trajectories of the evolution for either decreasing or increasing carbon. The color-shaded areas are the so-called basins of attraction, i.e. the set of initial conditions, starting in which trajectories come to the same stable equilibrium. The area denoted as the "cold desert" is the solution without vegetation on the planet. The equilibrium temperature is below the lower tolerable temperature, while the "hot desert" marks a solution with a temperature, which is too hot for the vegetation. The "hot green planet" and "cold green planet" are the non-trivial solutions with low and high vegetation densities, respectively.

Fig. 4: Bifurcation diagram of the "climate + biosphere" system. Black lines indicate trajectories of the evolution for either decreasing or increasing carbon. Color-shaded areas denote the basis of attraction of the stable equilibria.

Two hysteresis loops can be identified (Svirezhev et al., 2003). Starting with the "hot desert" the planet evolves in the following way: hot desert → hot green planet → cold green planet → cold desert. The transition "hot green planet → cold green planet" is accompanied by almost an explosive increase in vegetation biomass. Starting from the cold desert, however, a different path is realized: cold desert → hot green planet → hot desert. This means that a current state of the coupled climate-biosphere system depends on its history. The change from one to another equilibrium is done in a non-continuous way. The arrows in the diagram indicate non-continuous transitions. The rise of the hot green planet from the hot desert only is a continuous process.

3. Conclusions

• The evolution of the Earth system can be understood as a sequence of bifurcations.
• The number of equilibria increases with increasing complexity of the model.
• Small changes in temperature or vegetation could force a drastic change in the climate-vegetation system; a new equilibrium could be realized.

This research was part of the POEM core project at the Potsdam Institute for Climate Impact Research.

References

Esser, G., 1991. Osnabrück Biosphere Modelling and Modern Ecology.. In: G. Esser, D. Overdieck (Eds.). Modern Ecology, Basic and Applied Aspects. Elsevier, Amsterdam, 773-804.

Kostitzin, V. A., 1935. L' evolution de 'l atmosphere: Circulation organique, epoques glaciaries. Hermann, Paris.

Lüdeke, M. K. B., S. Dönges, R. D. Otto et al., 1995. Responses in NPP and carbon stores of the northern biomes to a CO₂-induced climatic change as evaluated by the Frankfurt biosphere model (FBM). Tellus 47B, 191-205.

Svirezhev, Y. M., 1994. Simple model of interaction between climate and vegetation: virtual biospheres, IIASA Seminar, Laxenburg.

Svirezhev, Y. M., and W. von Bloh, 1996. A minimal model of interaction between climate and vegetation: qualitative approach, Ecol. Mod. 92, 89-99 (abstract, full text in a HTML-document).

Svirezhev, Y. M., and W. von Bloh, 1997. Climate, vegetation, and global carbon cycle: the simplest zero-dimensional model , Ecol. Mod. 101, 79-95 (abstract, full text in a HTML-document).

Y. M. Svirezhev and W. von Bloh , 1999. The climate change problem and dynamical systems: virtual biospheres concept. In: G. Leitmann, F. E. Udwadia, A. V. Kryazhimski (eds.), Dynamics and control, Gordon and Breach, 161-173 (abstract).

Svirezhev, Y. M., A. Block and W. von Bloh, 2003. "Active planetary cover" concept and long-term evolution of planetary climate. In: W.E. Krumbein, D.M. Paterson and G.A. Zavarzin (eds.), Fossil and Recent Biofilms, A Natural History of Life on Earth, Kluwer Academic Publishers, Dordrecht/ Boston/ London, 415-427 (abstract).

Vernadsky, V., 1998. The Biosphere, Complete Annotated Edition. Springer, New York, 250 p..

von Bloh, W., A. Block, and H.-J. Schellnhuber, 1997. Self stabilization of the biosphere under global change: a tutorial geophysiological approach. Tellus 49B, 249-262 (abstract, full text as a HTML-document).

Watson, A. J., and J. E. Lovelock, 1983. Biological homeostasis of the global environment: the parable of Daisyworld . Tellus 35B, 286-289.