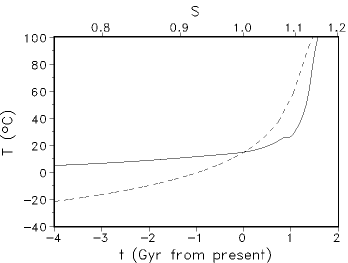
1. Basic concepts

The intention of geophysiological modelling is the analysis of the feedback mechanisms acting between geo- and biosphere (Lovelock, 1989, Lovelock, 1991). It is one approach to Earth System Analysis (Schellnhuber and Wenzel, 1998). The planet Earth can be understood as a "superorganism" which itself regulates to a state allowing life on Earth. (Gaia hypothesis, see, e.g., Lovelock and Margulis, 1974, Lenton, 1998). First attempts were done by Vernadsky (1927) on a qualitative level in the form of an idea about the interdependence between vegetation and climate (see, e.g., Vernadsky, 1998). Later on Kostitzin (1935) realized this idea in the first mathematical model for the coevolution of atmosphere and biota. So-called "minimal models" of the Earth are described in (Svirezhev and von Bloh, 1996, 1997). According to the "virtual biospheres" concept (Svirezhev and von Bloh, 1999) the evolution of the Earth system can be understood as a sequence of bifurcations.

An example of geophysiological regulation behaviour can be found in the Earth system: Silicate-rock weathering as a process to regulate the surface temperature. Due to silicate rock weathering carbon dioxide is taken out of the atmosphere. At geologic time scales there is an equilibrium between this sink of carbon and the sources by volcanic emissions. An increase in temperature accelerates the chemical processes of weathering reducing the amount of carbon in the atmosphere. Due to the lower greenhouse effect the temperature decreases; we have a negative feedback regulating the surface temperature.

Based on the work of Lovelock and Whitfield (1982) Caldeira and Kasting (1992) have developed a model to estimate the life span of the biosphere taken into account the above mentioned feedback mechanism. In Fig. 1 the global surface temperature is plotted under increase of the solar luminosity for the whole history of the Earth. In contrast to the curve for fixed carbon dioxide content of the atmosphere the temperature is always above the freezing point of water. Such a regulation mechanism can be an explanation for the "faint young Sun" paradox (Sagan and Mullen, 1972), where we have at least for 3.8 Gyr in the past always liquid water on the surface of Earth. The role of the biosphere is to increase the weathering rate.

The Caldeira/Kasting model assumes constant volcanic activity and continental area during the Earth evolution, Franck et al. (2000) extend this model by adding a geodynamic description of the geospheric processes. A short description of the model used can be found here. Such a model can be used to determine the habitability of Earth-like planets in the solar system and for extrasolar planetary systems.

Fig. 1: Evolution of the global surface temperature T for the Caldeira/Kasting model (solid curve) and a model with fixed (present) atmospheric CO₂ (dashed curve). S denotes the corresponding solar luminosity in solar units.

2. Model description

The basic characteristics of such feedback models can be illustrated using the "Daisyworld" scenario (Watson and Lovelock, 1983): In this model a planet with surface albedo A₀ can be covered by two types of vegetation: one species ("white daisies") with an albedo α₁> α₀ and the other species with albedo α₂ < α₀ ("black daisies") covering fraction N₁ and N₂ of the planetary surface normalized to one. Then the dynamic of the two daisies can be described by the following differential equations:

dN₁(t)/dt=N₁(&beta(T₁)x-γ)
dN₂(t)/dt=N₂(&beta(T₂)x-γ)
x=1-N₁-N₂,

where β(T) is the growth rate and γ the death rate of daisies. The global temperature is determined by the balance between ingoing solar radiation and outgoing black-body radiation

T=(S(1-&alpha)/4σ)^1/4,

where α=α₁N₁+&alpha₂N₂+&alpha₀x is the global albedo. Due to their different albedos the local temperatures T_1,2 differ from each other.

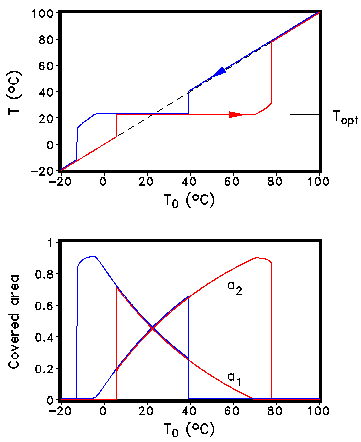
T₁⁴=T⁴+q(α-&alpha₁)
T₂⁴=T⁴+q(α-&alpha₂),

where the factor q depends on the heat exchange. The growth function β depends only on the local temperature T_1,2. Because the global albedo of the planet is changed by the growth process, the global temperature is changed altering the growth rates.

One interesting aspect is the behaviour of the coupled vegetation-climate model on external perturbations, e.g., an increase of the external solar luminosity. In Fig. 2 the solar luminosity was successively increased. It must be pointed out that the global temperature of the populated planet - in contrast to the unpopulated one - is remarkable constant in a wide range of solar luminosity: the planet itself regulates the optimum state of life (homeostasis).

The original Daisyworld model has been analyzed by other authors in great detail, informations can be found in Isakari and Somerville (1989) and Saunders (1994).

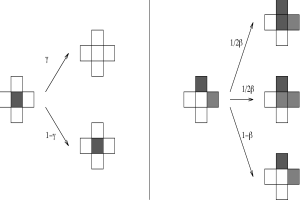
Fig. 2: Coevolution of climate and vegetation at increasing (red) and decreasing (blue) insolation. T₀ is the global temperature of the corresponding planet without vegetation.

3. Two-dimensional multi species approach

The conceptual simple zero-dimensional Daisyworld model allows in an equilibrium state due to theoretical considerations only the coexistence of at most two different species. This restriction can be avoided if we introduce spatial dependency into the model. The local temperatures T₁, T₂ and albedos α₁, α₂ are replaced by 2-dimensional fields T(x,y) and α(x,y). The temporal and spatial evolution of the temperature is determined by a partial differential equation based on an energy-balance model (EBM) (see, e.g., Henderson-Sellers and McGuffie, 1983). The evolution of the albedo connected directly with the vegetation is modelled by a cellular automaton (CA) approach (for a description of the Cellular automaton concept see, e.g., Wolfram, 1983, Goles, 1994). CA models have been successfully applied to a variety of problems. An application of such a CA approach to the modelling of calcite formation in microbial mats is presented in (Kropp et al., 1996). Fig. 3 describes the non-deterministic rules for the update of the lattice.

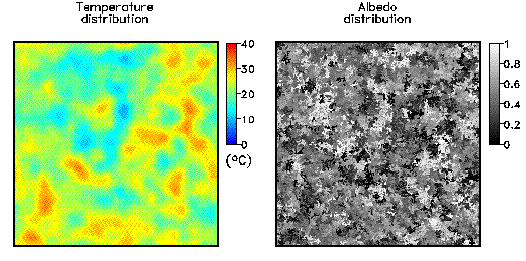
Fig. 3: Update rules for the cellular automaton for an empty cell(right-hand side) and a covered cell (left-hand side). The state of the cell in the following time step depends only on the state of the cell itself and their next neighbours.

The model was implemented on a RS/6000 SP parallel computer (IBM). Because of only next-neighbour interactions a high efficiency of the parallelization can be expected. The parallelization was performed using the GeoPar library based on the message-passing paradigm. Some documentation and links about parallel programming can be found here.

A typical state of the temperature and albedo distribution is plotted in Fig. 4.

Fig. 4: Typical configuration for the albedo distribution (right-hand side) and the temperature distribution (left-hand side).

The 2-dimensional model has a similar self-regulation behaviour as the original model. Due to the cellular automaton approach the model can be simply extended to incorporate several biological effects like

1. mutations
2. seeding
3. habitat fragmentation

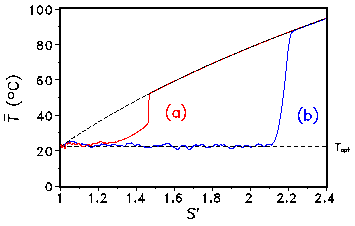
into the model. Only the set of rules defining the CA must be modified. One expects that adding mutations, i.e., slight random changes of the albedo in the growth process, will decrease the regulation capability. But after doing the simulation one gets a counter-intuitive result: with mutations the solar luminosity can be significantly increased until the vegetation breaks down (see Fig. 5).

Fig. 5: Global temperature T vs. increasing insolation S with (b) and without (a) mutation of the albedo.

An animation is available as a MPEG video(11 MByte). It illustrates the temperature and albedo evolution under increasing insolation. After the vegetation is wiped out the insolation is decreased:

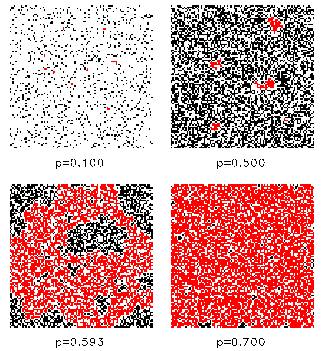
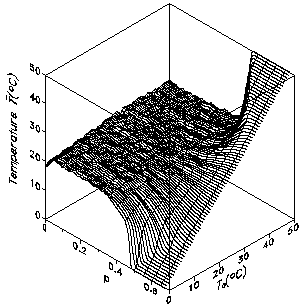
It can be clearly seen that the CA version of the Daisyworld exhibits hysteresis, i.e. the behaviour of the model depends on its history. The breakdown of the vegetation is a first-order phase transition. This model has also been used by Ackland et al. (2003) in order to describe the formation of deserts in Daisyiworld.

4. Fragmentation of growth area

In the real world the growth area is not simply connected, but is fragmented due to anthropogenic influences by, e.g., human settlements and infrastructure. It is possible to model such fragmentations with our 2-dimensional CA and to analyze the effects on the regulation capability.

The fragmentation is modelled by a percolation model (Stauffer and Aharony, 1992). In each time step a cell can be marked as "infertile" with a given probability p independent of its state. Configurations for different concentrations p of infertile cells are shown in Fig. 6:

Fig. 6: Fragmentation of landscape for different concentrations of infertile cells p. Some connected clusters are marked (red color).

For a critical p an infinite cluster of connected cells is formed. At 1-p the growth area splits up into disconnected areas. The critical concentration p_c can be numerically determined to p_c=0.537...

The simulations of the 2-dimensional Daisyworld model with fragmentation are done for different constant solar luminosities S. The regulation capability breaks down at p=0.407 independent of the initial solar luminosity S. More details can be found in (von Bloh et al., 1997).

Fig. 7: Global average temperature as a function of the fragmentation p and the temperature T₀ of the uncovered planet.

5. Introducing herbivores into Daisyworld

In order to reflect the fundamental ecosystems dynamics on trophic interactions as well, we extend the 2D model even further and add herbivores to our planet (see also, e.g., Harding and Lovelock, 1996). These vegetarian "lattice animals" move on the grid as random walkers. The state of the herbivore can be changed by four different events:

Death

The herbivore deceases with a certain probability γ_h.

Ingestion

If the herbivore survive and if the cell is covered by a daisy then the animal consumes the plant.

Reproduction

The herbivore in question may give birth to a "lattice child". The probability of such an event depends on the local temperature and the number of daisies "eaten" by the herbivore in a multiplicative manner.

Move

The herbivore may also walk to a randomly chosen next neighbour cell if the cell is not already occupied by another herbivore.

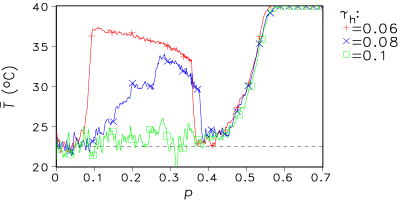
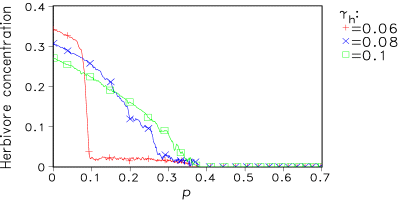
Fig. 8 shows some results for increasing fragmentation at different mortality rates γ_h for the herbivores. In von Bloh et al. (1999) the Daisyworld model including herbivores is described in detail.

(a)

(b)

Fig. 8: (a) Dependence of global mean temperature T on fragmentation parameter p for distinct herbivore mortality rates γ_h. (b) Dependence of herbivore concentration on p for the same mortality rates as in (a).

6. Conclusions

Starting from a very simple geophysiological model the developed 2-D model shows some remarkable effects:

• Local interactions of competing species lead to global effects: Self organized regulation behaviour of the global temperature under external perturbations.
• The system undergoes a first order phase transition: After the regulation capability is exhausted, an irreversible breakdown occurs immediately.
• By splitting the growth area into disconnected regions via, e.g., successive fragmentation the regulation behaviour also breaks down.

This research was part of the POEM core project at the Potsdam Institute for Climate Impact Research.

References

Ackland, G. J., M. A. Clark, and T. M. Lenton, 2003. Catastrophic desert formation in Daisyworld. J. Theo. Biol. 223(1), 39-44.

Caldeira, K., and J. F. Kasting, 1992. The life span of the biosphere revisited. Nature 360, 721-723.

Esser, G., 1991. Osnabrück Biosphere Modelling and Modern Ecology. In: G. Esser, D. Overdieck (Eds.). Modern Ecology, Basic and Applied Aspects. Elsevier, Amsterdam, 773-804.

Franck, S., A. Block, W. von Bloh, C. Bounama, H.-J. Schellnhuber, and Y. M. Svirezhev, 2000. Reduction of life span as a consequence of geodynamics. Tellus 52B, 94-107 (abstract, full text as a HTML-document).

Goles, E., (Ed.), 1994. Cellular automata, dynamical systems and neural networks . Kluwer Acad. Pub., Dordrecht.

Harding, S. P., and J. E. Lovelock, 1996. Exploiter mediated coexistence and frequency-dependent selection in a geophysiological model. J. Theor. Biol. 182, 109-116.

Lüdeke, M. K. B., S. Dönges, R. D. Otto, et al. , 1995. Responses in NPP and carbon stores of the northern biomes to a CO₂-induced climatic change as evaluated by the Frankfurt biosphere model (FBM). Tellus 47B, 191-205.

Henderson-Sellers, A., and K. Mc Guffie, 1983. A climate modelling primer. John Wiley & Sons, Chichester.

Isakari, S. M., and R. C. J. Somerville, 1989. Accurate numerical solutions for Daisyworld. Tellus 41B, 478-482.

Kostitzin, V. A., 1935. L' evolution de 'l atmosphere: Circulation organique, epoques glaciaries. Hermann, Paris.

Kropp, J., W. von Bloh, and T. Klenke, 1996. Calcite formation in microbial mats: modeling and quantification of inhomogeneous distribution patterns by a cellular automaton model and multifractal measures. Geol. Rundsch. 85, 857-863 (abstract).

Lenton, T. M., 1998. Gaia and natural selection. Nature 394, 439-447.

Lovelock, J. E., and M. Whitfield, 1982. Life span of biosphere. Nature 296, 561-563.

Lovelock, J. E., 1989. The ages of Gaia. Oxford University Press, Oxford.

Lovelock, J. E., 1991. GAIA - the practical science of planetary medicine. GAIA books, London.

Lovelock, J. E., and L. Margulis, 1974. Atmospheric homeostasis by and for the biosphere: the Gaia hypothesis. Tellus 26, 2-10.

Sagan, C., and G. Mullen, 1972. Earth and Mars: Evolution of atmospheres and surface temperatures. Science 177, 52-56.

Saunders, P. T., 1994. Evolution without natural selection: Further implications of the Daisyworld parable. J. theor. Biol. 166 (4), 365-373.

Schellnhuber, H.-J., and V. Wenzel (eds.), 1998. Earth System Analysis: Integrating Science for Sustainability. Springer, Berlin (abstract).

Stauffer, D., and A. Aharony, 1992. Introduction to Percolation Theory, 2nd ed.. Taylor and Francis, London.

Svirezhev, Y. M., 1994. Simple model of interaction between climate and vegetation: virtual biospheres. IIASA Seminar, Laxenburg.

Svirezhev, Y. M., and W. von Bloh, 1996. A minimal model of interaction between climate and vegetation: qualitative approach. Ecol. Mod. 92, 89-99 (abstract, full text in a HTML-document).

Svirezhev, Y. M., and W. von Bloh, 1997. Climate, vegetation, and global carbon cycle: the simplest zero-dimensional model . Ecol. Mod. 101, 79-95 (abstract, full text in a HTML-document).

Svirezhev, Y. M., and W. von Bloh, 1999. The climate change problem and dynamical systems: virtual biospheres concept. In: G. Leitmann, F. E. Udwadia, A. V. Kryazhimski (Eds.). Dynamics and control. Gordon and Breach, 161-173 (abstract).

Vernadsky, V., 1998. The Biosphere, Complete Annotated Edition. Springer, New York, 250 p..

von Bloh, W., A. Block, and H.-J. Schellnhuber, 1997. Self stabilization of the biosphere under global change: a tutorial geophysiological approach. Tellus 49B, 249-262 (abstract, full text as a HTML-document).

von Bloh, W., A. Block, M. Parade, and H.-J. Schellnhuber, 1999. Tutorial modelling of geosphere-biosphere interactions: the effect of percolation-type habitat fragmentation. Physica A 226, 186-196 (abstract, full text as a HTML-document).

Watson, A. J., and J. E. Lovelock, 1983. Biological homeostasis of the global environment: the parable of Daisyworld . Tellus 35B, 286-289.

Wolfram, S., 1986. Theory and Applications of Cellular Automata. World Scientific, Singapore.