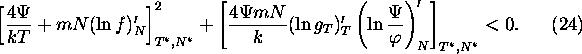Let us consider the point
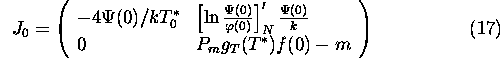
and the corresponding eigenvalues are equal to:
i.e. this equilibrium is a stable node, if
and it is an unstable saddle, if
Since
After linearization of the system (6)-(7) in the vicinity of the equilibrium points,
we get the Jacobi matrix:

Let us consider the point ![]() . Then
. Then
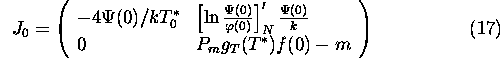
and the corresponding eigenvalues are equal to:
![]()
i.e. this equilibrium is a stable node, if
![]()
and it is an unstable saddle, if
![]()
Since ![]() for any
for any ![]() , then
, then ![]() , and
any equilibrium
, and
any equilibrium ![]() is stable.
is stable.
If ![]() then
then
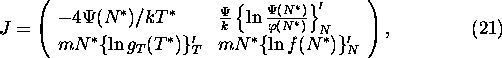
and the corresponding eigenvalues are equal to
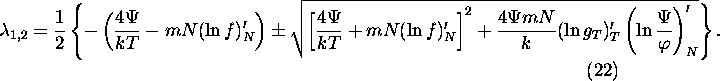
Since ![]() for any
for any ![]() , then
, then
![]() , and the equilibrium with
, and the equilibrium with ![]() cannot be an unstable node.
cannot be an unstable node.
This equilibrium is a saddle point if
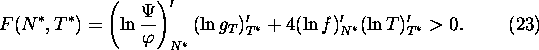
If ![]() , we have a stable node or stable focus, moreover
for the latest
, we have a stable node or stable focus, moreover
for the latest