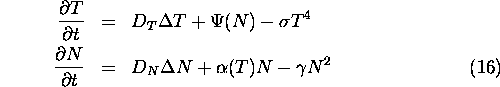
Since inhomogeneous equilibrium solutions do not exist, we can restrict to wave solutions of (16), i.e. solutions in the form
where
``Revenons à nos moutons'', i.e. let us consider the original problem again: There is the system
of two nonlinear parabolic equations:
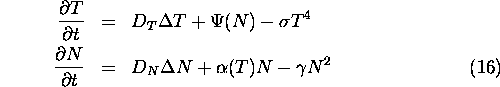
Since inhomogeneous equilibrium solutions do not exist, we can restrict to wave solutions of (16), i.e. solutions in the form
![]()
where ![]() is the velocity of wave, to study the propagation of
perturbations and,
secondly, to special class of initial conditions, which will generate these waves:
is the velocity of wave, to study the propagation of
perturbations and,
secondly, to special class of initial conditions, which will generate these waves:
![]() and
and ![]() must be finite functions, i.e. they differ
out of zero only on a finite interval.
must be finite functions, i.e. they differ
out of zero only on a finite interval.
If we substitute into (16) the form (17) then we get (let ![]() ):
):
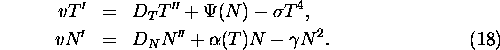
This 2-dimensional system of second order ordinary differential equations can be transformed
into a 4-dimensional first-order system if we add two phase variables
p, q:
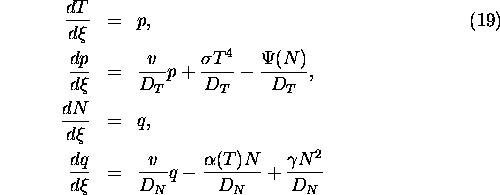
At the equilibria of (19) p and q must be zero. Then the equilibria
of (4) are also equilibria of the two remaining
equations of (19).
But mention that the system dimensions are distinct.
In the remaining part of our paper we will focus on the development of such propagating waves under different initial conditions of T and N. It is necessary to solve (19) explicitly, which cannot be done analytically due to the nonlinearity of the system. Therefore further analysis of the system is carried out with numerical methods.
The original system (16) was solved for different initial conditions of the form:
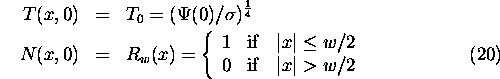
N(x,0) is defined on a finite carrier [-w/2,w/2] and could be member of
the class of initial perturbations generating nonlinear waves.
From now on N(x,t), T(x,t) are defined on a finite world ![]() . Therefore
the behaviour of the model must be defined at the boundaries x=-L,L.
We choose periodic boundary conditions
. Therefore
the behaviour of the model must be defined at the boundaries x=-L,L.
We choose periodic boundary conditions
![]()
defining a ring topology on ![]() .
.
The numerical calculations were done with an adaptive Runge-Kutta scheme after transforming the
partial differential equations by a finite difference method into a system of ordinary
ones. For a short description of the applied algorithms
see, e.g., [14]).
These calculations were repeated for a set of parameters w and ![]() , i.e. different insolation
, i.e. different insolation ![]() , on the domain
, on the domain ![]() and the
following was observed:
and the
following was observed:
If ![]() the evolution in time depends on the parameter w (the width of
the rectangular initial condition for N as defined in (20)) (see Fig. 6a,b).
the evolution in time depends on the parameter w (the width of
the rectangular initial condition for N as defined in (20)) (see Fig. 6a,b).
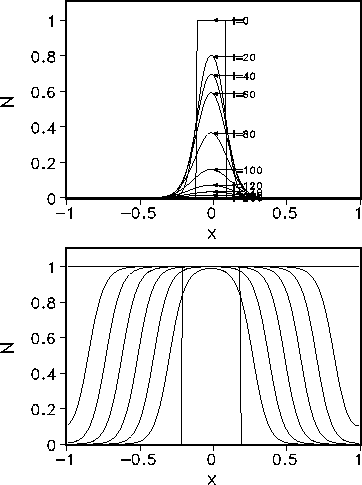
Figure 6: Evolution in time of the vegetation N(x,t) for a rectangular perturbation
with (a) ![]() , (b)
, (b) ![]() . The labels at the curves in (a) denote the different
times t. The equidistant curves in (b) indicate a constant propagation velocity of the nonlinear waves.
. The labels at the curves in (a) denote the different
times t. The equidistant curves in (b) indicate a constant propagation velocity of the nonlinear waves.
If w is below a critical value ![]() , then the solution N(x,t) vanishes in time, i.e.:
, then the solution N(x,t) vanishes in time, i.e.:
![]()
For ![]() , however, a propagation of the initial perturbation with a constant velocity v can be observed (see Fig. 6b).
, however, a propagation of the initial perturbation with a constant velocity v can be observed (see Fig. 6b).
An explanation of this behaviour can be found if we compare the system with
the equivalent system of the uniform biosphere: At the chosen ![]() two
equilibria are stable with
two
equilibria are stable with ![]() and
and ![]() (see Fig. 5b). It depends on the initial
value of N which of the two equilibria are reached. The diffusive system
exhibits a similar behaviour because the final state depends on the width of
the initial perturbation.
(see Fig. 5b). It depends on the initial
value of N which of the two equilibria are reached. The diffusive system
exhibits a similar behaviour because the final state depends on the width of
the initial perturbation.
As a first guess, the total amount of vegetation N, described by
![]()
seems to be an appropriate criterion for the development of propagating waves.
However, this is not valid,
the geometrical arrangement must also be taken into account. To
prove this a composition of two rectangular perturbations (![]() ,
, ![]() )
separated by a distance
)
separated by a distance ![]() was used as an
initial configuration:
was used as an
initial configuration:
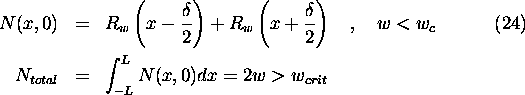
Note that each of the rectangular perturbations ![]() alone
(
alone
(![]() ) goes to zero for
) goes to zero for ![]() . For
. For ![]() , however, we have
, however, we have
![]()
which propagates in time with nonlinear waves.
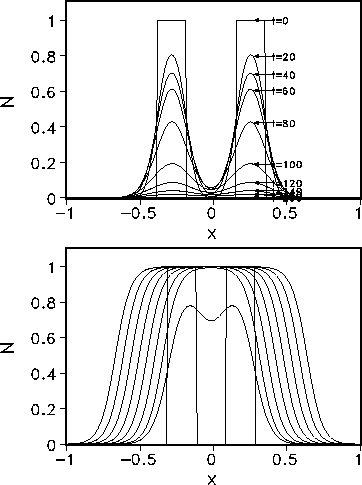
Figure: Development of the initial perturbation according to eq. 24 for (a) large ![]() and (b) small
and (b) small ![]() .
.
A development of propagating waves occurs even for ![]() (Fig. 7b), while
for large
(Fig. 7b), while
for large ![]() the perturbation vanishes in time (Fig. 7a).
the perturbation vanishes in time (Fig. 7a).